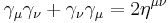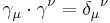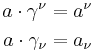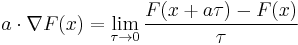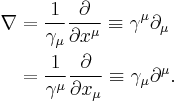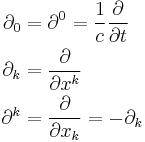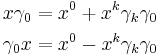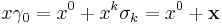Spacetime algebra
In mathematical physics, spacetime algebra (STA) is a name for the Clifford algebra Cℓ1,3(R),or Geometric algebra G4 = G(M4) which can be particularly closely associated with the geometry of special relativity and relativistic spacetime.
It is a linear algebra allowing not just vectors, but also directed quantities associated with particular planes (for example: areas, or rotations) or associated with particular (hyper-)volumes to be combined, as well as rotated, reflected, or Lorentz boosted. It is also the natural parent algebra of spinors in special relativity. These properties allow many of the most important equations in physics to be expressed in particularly simple forms; and can be very helpful towards a more geometrical understanding of their meanings.
Contents |
Structure
The spacetime algebra is built up from combinations of one time-like basis vector 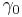 and three orthogonal space-like vectors,
and three orthogonal space-like vectors, 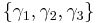 , under the multiplication rule
, under the multiplication rule
where 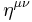 is the Minkowski metric with signature (+ − − −)
is the Minkowski metric with signature (+ − − −)
Thus 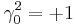 ,
, 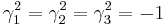 , otherwise
, otherwise 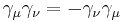 .
.
The basis vectors 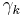 share the same properties as the Dirac matrices, but no explicit matrix representation is utilized in STA.
share the same properties as the Dirac matrices, but no explicit matrix representation is utilized in STA.
This generates a basis of one scalar, 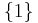 , four vectors
, four vectors 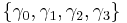 , six bivectors
, six bivectors 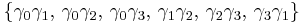 , four pseudovectors
, four pseudovectors 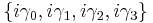 and one pseudoscalar
and one pseudoscalar 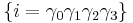 .
.
Reciprocal frame.
Associated with the basis 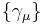 is the reciprocal basis
is the reciprocal basis 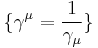 , satisfying the relation
, satisfying the relation
These reciprocal frame vectors differ only by a sign, with 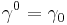 , and
, and 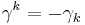 .
.
A vector may be represented in either upper or lower index coordinates 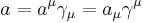 , where the coordinates may be extracted by taking dot products with the basis vectors or their reciprocals
, where the coordinates may be extracted by taking dot products with the basis vectors or their reciprocals
Space time gradient
The spacetime gradient, like the gradient in a Euclidean space, is defined such that the directional derivative relationship is satisfied
One can show that this requires the definition of the gradient to be
Written out explicitly with 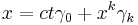 , these partials are
, these partials are
Space time split
Pre or post multiplication by the time like basis vector 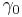 serves to split a four vector into a scalar timelike and a bivector spacelike component. With
serves to split a four vector into a scalar timelike and a bivector spacelike component. With 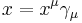 we have
we have
As these bivectors 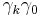 square to unity, they serve as a spatial basis. Utilizing the Pauli matrix notation, these are written
square to unity, they serve as a spatial basis. Utilizing the Pauli matrix notation, these are written 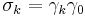 . Spatial vectors in STA are denoted in boldface; for the spacetime split
. Spatial vectors in STA are denoted in boldface; for the spacetime split 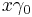 one therefore writes
one therefore writes
where 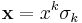 .
.
Multivector division
The spacetime algebra is not a formal division algebra, because it contains idempotents 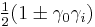 and zero divisors:
and zero divisors: 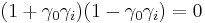 . These can be interpreted as projectors onto the light-cone and orthogonality relations for such projectors, respectively. But in general it is possible to divide one multivector quantity by another, and make sense of the result: so, for example, a directed area divided by a vector in the same plane gives another vector, orthogonal to the first.
. These can be interpreted as projectors onto the light-cone and orthogonality relations for such projectors, respectively. But in general it is possible to divide one multivector quantity by another, and make sense of the result: so, for example, a directed area divided by a vector in the same plane gives another vector, orthogonal to the first.
In relativistic quantum mechanics
The relativistic quantum wavefunction is sometimes expressed as a spinor field, i.e.
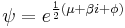
where ϕ is a bivector, so that
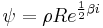
where R is viewed as a Lorentz rotation; David Hestenes interprets this equation as connecting spin with the imaginary pseudoscalar, and others have extended this to provide a framework for locally varying vector- and scalar-valued observables and support for the Zitterbewegung interpretation of quantum mechanics originally proposed by Schrödinger.
In a new formulation of General Relativity
Lasenby, Doran, and Gull of Cambridge University have proposed a new formulation of gravity, termed Gauge-Theory Gravity (GTG), wherein Spacetime Algebra is used to induce curvature on Minkowski space while admitting a gauge symmetry under "arbitrary smooth remapping of events onto spacetime" (Lasenby, et al.); a nontrivial proof then leads to the geodesic equation,
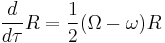
and the covariant derivative
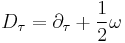 ,
,
where ω is the connexion associated with the gravitational potential, and Ω is an external interaction such as an electromagnetic field.
The theory shows some promise for the treatment of black holes, as its form of the Schwarzschild solution does not break down at singularities; most of the results of General Relativity have been mathematically reproduced, and the relativistic formulation of classical electrodynamics has been extended to quantum mechanics and the dirac equation.
See also
References
- A. Lasenby, C. Doran, & S. Gull, “Gravity, gauge theories and geometric algebra,” Phil. Trans. R. Lond. A 356: 487–582 (1998).
- Chris Doran and Anthony Lasenby (2003). Geometric Algebra for Physicists, Cambridge Univ. Press. ISBN 0-521-48022-1
- David Hestenes (1966). Space-Time Algebra, Gordon & Breach.
- David Hestenes and Sobczyk, G. (1984). Clifford Algebra to Geometric Calculus, Springer Verlag ISBN 90-277-1673-0
- David Hestenes (1973). "Local observables in the Dirac theory", J. Math. Phys. Vol. 14, No. 7.
- David Hestenes (1967). "Real Spinor Fields", Journal of Mathematical Physics, 8 No. 4, (1967), 798–808.